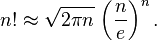Reputation: 7769

Can one know how large a factorial would be before calculating it?

I'm using GMP to calculate very large factorials (e.g. 234234!). Is there any way of knowing, before one does the calculation, how many digits long the result will (or might) be?

Upvotes: 3

Answers (6)

Michael Borgwardt

Reputation: 346310

You can transform Stirling's approximation formula using simple logarithmic math to get you the number of digits:

n!         ~ sqr(2*pi*n) * (n/e)^n
log10(n!)  ~ log10(2*pi*n)/2 + n*log10(n/e)

Hardware float math is sufficient for this, which makes it lightning fast.

Upvotes: 12

Christian C. Salvadó

Reputation: 827396

The logarithm of the factorial can be used to calculate the number of digits that the factorial number will take:

logn!

This can be easily translated to an algorithmic form:

//Pseudo-code
function factorialDigits (n) 
  var result = 0;

  for(i = 1; i<=n; i++)
    result += log10(n);

  return result;

Upvotes: 7

Ratnesh Maurya

Reputation: 706

it would be

nlog(n) - n + log(n(1 + 4n(1 + 2n)))/6 + log(pi)/2

see topic "rate of growth" @ http://en.wikipedia.org/wiki/Factorial Srinivasa Ramanujan method

Upvotes: 2

user2189331

Reputation:

Well about four people have mentioned Stirling so... another option is a LUT storing the number of digits for each of the first N factorials. Assuming 4 bytes for the integer and 4 bytes for the number of digits, you could store the first 1,000,000 factorials in around 8MB.

Upvotes: 1