CODEWITHSUNDEEP
rggplot2
isDotR
isDotR

Reputation: 1063

Transform color scale, but keep a nice legend with ggplot2

I have seen somewhat similar questions to this, but I'd like to ask my specific question as directly as I can:

I have a scatter plot with a "z" variable encoded into a color scale:

library(ggplot2)
myData <- data.frame(x = rnorm(1000),
                     y = rnorm(1000))
myData$z <- with(myData, x * y)

badVersion <- ggplot(myData,
              aes(x = x, y = y, colour = z))
badVersion <- badVersion + geom_point()
print(badVersion)

Which produces this: 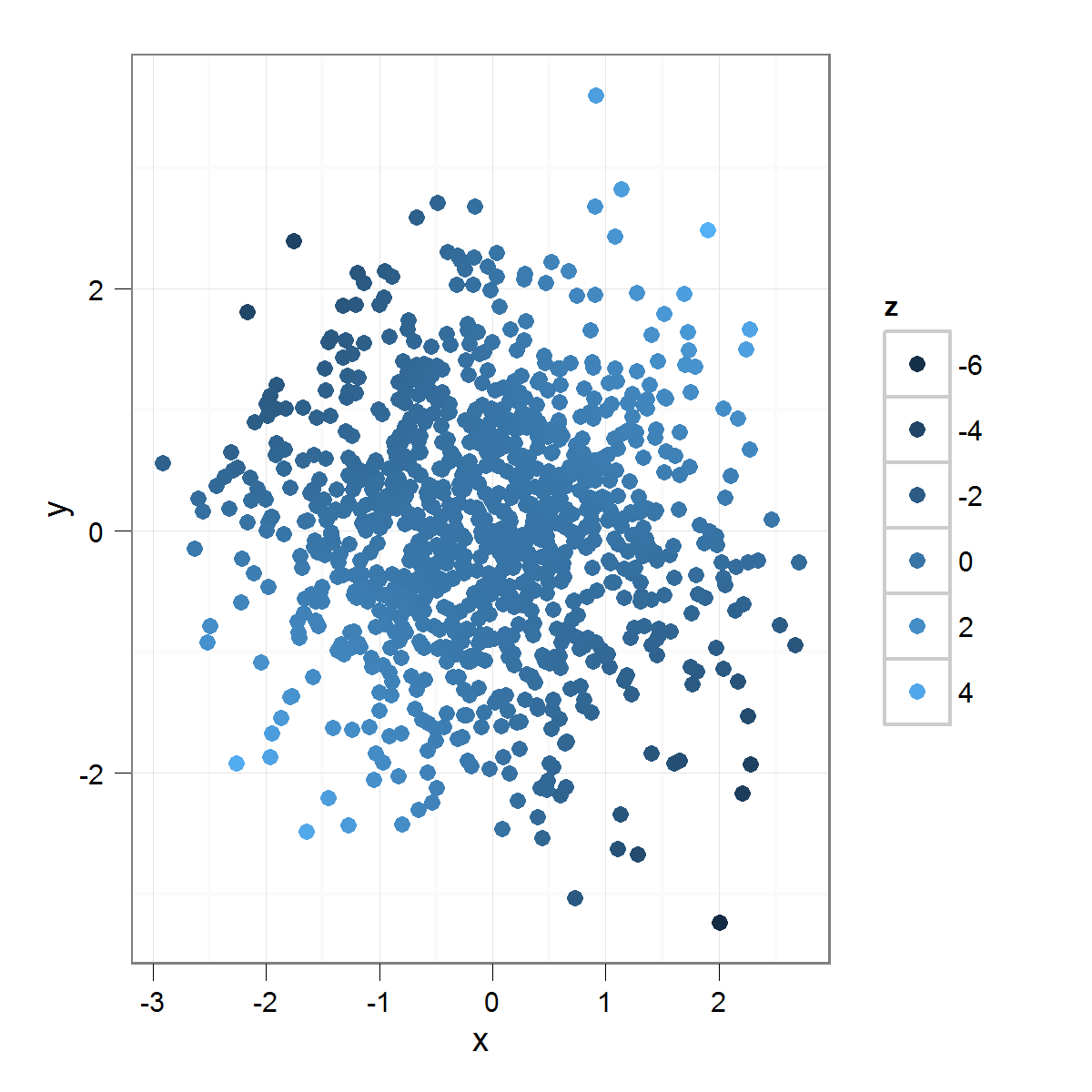bad version

As you can see, since the "z" variable is normally distributed, very few of the points are colored with the "extreme" colors of the distribution. This is as it should be, but I am interested in emphasizing difference. One way to do this would be to use:

betterVersion <- ggplot(myData,
                        aes(x = x, y = y, colour = rank(z)))
betterVersion <- betterVersion + geom_point()
print(betterVersion)

Which produces this: 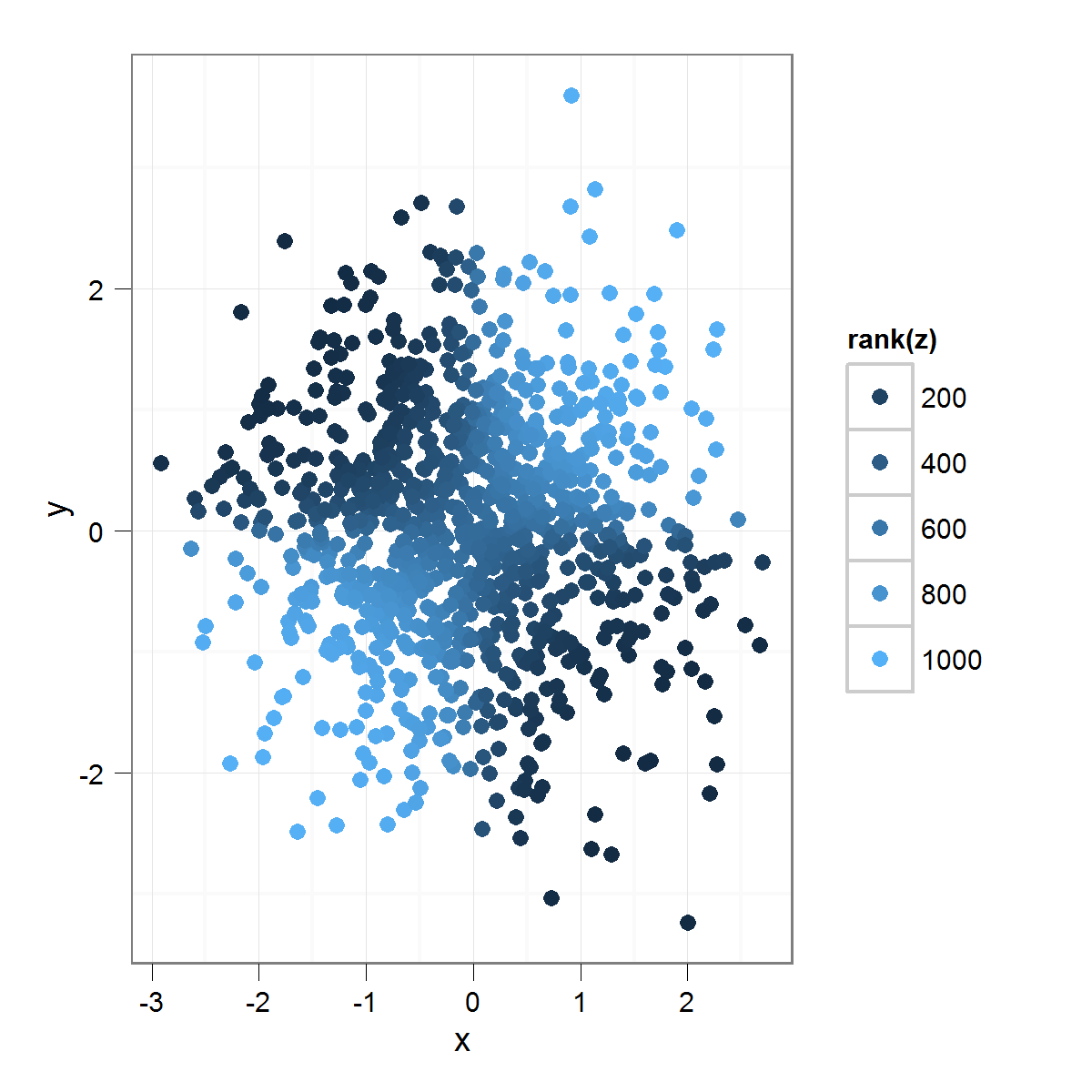better version

By applying rank() to the "z" variable, I get a much greater emphasis on minor differences within the "z" variable. One could imagine using any transformation here, instead of rank, but you get the idea.

My question is, essentially, what is the most straightforward way, or the most "true ggplot2" way, of getting a legend in the original units (units of z, as opposed to the rank of z), while maintaining the transformed version of the colored points?

I have a feeling this uses rescaler() somehow, but it is not clear to me how to use rescaler() with arbitrary transformations, etc. In general, more clear examples would be useful.

Thanks in advance for your time.

Upvotes: 16

Views: 3031

Answers (1)

mnel
mnel

Reputation: 115435

Have a look at the package scales especially ?trans

I think that a transformation that maps the colour given the probability of getting the value or more extreme should be reasonable (basically pnorm(z))

I think that scale_colour_continuous(trans = probability_trans(distribution = 'norm') should work, but it throws warnings.

So I defined a new transformation (see ?trans_new)

I have to define a transformation and an inverse

library(scales)
norm_trans <- function(){
  trans_new('norm', function(x) pnorm(x), function(x) qnorm(x))
}

badVersion + geom_point() + scale_colour_continuous(trans = 'norm'))

enter image description here

Using the supplied probability_trans throws a warning and doesn't seem to work

# this throws a warning
badVersion + geom_point+
  scale_colour_continuous(trans = probability_trans(distribution = 'norm'))

## Warning message:
## In qfun(x, ...) : NaNs produced

enter image description here

Upvotes: 10

Related Questions