Algorithm in hardware to find out if number is divisible by five

Question

I am trying to think of an algorithm to implement this for a given n bit binary number. I tried out many examples, but am unable to find out any pattern. So how shall I proceed?

Answer 1

Well, I just figured out ...
number mod 5 = a0 * 2^0 mod 5 + a1 * 2^1 mod 5 +a2* 2^2 mod 5 + a3 * 2^3 mod 5 + a4 * 2^4 mod 5 + ....
= a0(1)+a1(2) + a2(-1)+a3(-2) + a4(1) repeats ...

Hence difference of odd digits + 2 times difference of even digits = divisible by 5

for example ... consider 110010
odd digits difference = 0-0+1 = 1 or 01
even digits difference = 1-0+1 = 2 or 10

difference of odd digits + 2 times difference of even digits
= 01 + 2*(10)
= 01 + 100
= 101 is divisible by 5.

Answer 2

We can design a Deterministic Finite Automaton (DFA) for the same. The DFA, then can be implemented in Hardware. This is similar to this answer.

We will simulate a Deterministic Finite Automaton (DFA) that accepts Binary Representation of Integers which are divisible by 5

Now, by accept, we mean that when we are done with scanning string, we should be in one of the multiple possible Final States.

---

Approach to Design DFA : Essentially, we need to divide the Binary Representation of Integer by 5, and track the remainder. If after consuming/scanning [From Left to Right] the entire string, remainder is Zero, then we should end up in Final State, and if remainder isn't zero we should be in Non-Final States.

Now, DFA is defined by Quintuple/5-Tuple (Q,q₀,F,Σ,δ). We will obtain these five components step-by-step.

1. Q : Finite Set of States
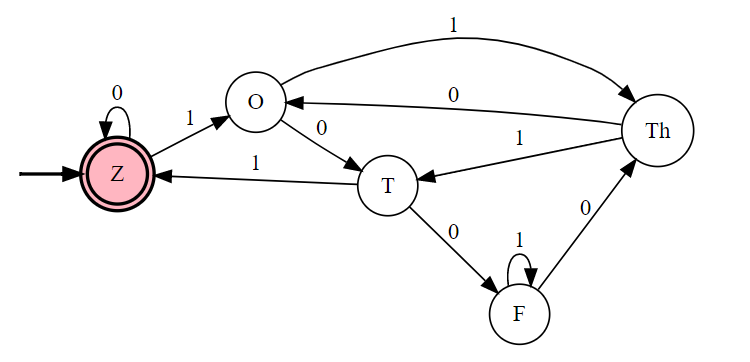
   We need to track remainder. On dividing any integer by 5, we can get remainder as 0,1, 2, 3 or 4. Hence, we will have Five States Z, O, T, Th and F for each possible remainder.
   Q={Z, O, T, Th, F}
   If after scanning certain part of Binary String, we are in state Z, this means that integer defined from Left to this part will give remainder Zero when divided by 5. Similarly, O for remainder One, and so on.
   Now, we can write these three states by Euclidean Division Algorithm as

Z : 5m
O : 5m+1
T : 5m+2
Th : 5m+3
F : 5m+4

where m is Integer.

2. q₀ : an initial/start state from set Q
   Now, start state can be thought in terms of empty string (ɛ). An ɛ directly gets into q₀.

What remainder does ɛ gives when divided by 5?
We can append as many 0s in left hand side of a Binary Number. In the similar fashion, we can append ɛ in left hand side of a Binary String. Thus, ɛ in left can be thought of as 0. And 0 when divided by 5 gives remainder 0. Hence, ɛ should end in State Z. But ɛ ends up in q₀.

Thus, q₀=Z

3. F : a set of accept states
   Now we want all strings which are divisible by 5, or which gives remainder 0 when divided by 5, or which after complete scanning should end up in state Z, and gets accepted. Hence,
   F={Z}
   
   

4. Σ : Alphabet (a finite set of input symbols)
   Since we are scanning/reading a Binary String. Hence,
   Σ={0,1}
   
   

5. δ : Transition Function (δ : Q × Σ → Q) Now this δ tells us that if we are in state x (in Q) and next input to be scanned is y (in Σ), then at which state z (in Q) should we go.
   If the string upto this point gives remainder 3/Th when divided by 5, and if we append 1 to string, then what remainder will resultant string give.
   
   
   Now, this can be analyzed by observing how magnitude of a binary string changes on appending 0 and 1.
   
   a.
   In Decimal (Base-10), if we add/append 0, then magnitude gets multiplied by 10 . 53, on appending 0 it becomes 530
   Also, if we append 8 to decimal, then Magnitude gets multiplied by 10, and then we add 8 to multiplied magnitude.
   
   b.
   In Binary (Base-2), if we add/append 0, then magnitude gets multiplied by 2 (The Positional Weight of each Bit get multiplied by 2)
   Example : (1010)₂ [which is (10)₁₀], on appending 0 it becomes (10100)₂ [which is (20)₁₀]
   
   Similarly, In Binary, if we append 1, then Magnitude gets multiplied by 2, and then we add 1.
   Example : (10)₂ [which is (2)₁₀], on appending 1 it becomes (101)₂ [which is (5)₁₀]
   
   Thus, we can say that for Binary String x,

• x0=2|x|
• x1=2|x|+1
  
  We will use these relation to analyze Five States
  
  Any string in Z can be written as 5m
- On 0, it becomes 2(5m), which is 5(2m), nothing but state Z.
  - On 1, it becomes 2(5m)+1, which is 5(2m)+1, that is O. [This can be read as if a Binary String is presently divisible by 5, and we append 1, then resultant string will give remainder as 1]
  
  
  Any string in O can be written as 5m+1
- On 0, it becomes 2(5m+1) = 10m+2, which is 5(2m)+2, state T.
  - On 1, it becomes 2(5m+1)+1 = 10m+3, which is 5(2m)+3, that is state Th.
  
  
  Any string in T can be written as 5m+2 - On 0, it becomes 2(5m+2) = 10m+4, which is 5(2m)+4, state F.
  - On 1, it becomes 2(5m+2)+1 = 10m+5, which is 5(2m+1), state Z. [If m is integer, so is (2m+1)]
  
  
  Any string in Th can be written as 5m+3
- On 0, it becomes 2(5m+3) = 10m+6, which is 5(2m+1)+1, state V.
  - On 1, it becomes 2(5m+3)+1 = 10m+7, which is 5(2m+1)+2, that is state T.
  
  
  Any string in F can be written as 5m+4
- On 0, it becomes 2(5m+4) = 10m+8, which is 5(2m+1)+3, state Th.
  - On 1, it becomes 2(5m+4)+1 = 10m+9, which is 5(2m+1)+4, that is state F.

---

Hence, the final DFA combining Everything (creating using Tool)

We can even write code [in High Level Language] for the same. But it would go beyond main aim of this question. If readers wish to see the same, they can check here.

---

Answer 3

As any assignment this would have been an answer for is bound to be way overdue a year later:
in the binary representation of a natural divisible by five the parities of bits 4n and 4n+2 equal, as well as those for bits 4n+1 and 4n+3.
(This is entirely equivalent to the answers of JoshG79, notsogeek, or james: 4≡-1(mod 5), 3≡-2(mod 5) (with reduced hand-waving about recursion in argumentation, and no dispensable handling of carries in circuitry))

Answer 4

The contribution of each bit toward being divisible by five is a four bit pattern 3421. You could shift through any binary number 4 bits at a time adding the corresponding value for positive bits.

Example:

100011

take 0011 apply the pattern 0021 sum 3

next four bits 0010 apply the pattern 0020 sum = 5

Answer 5

Make a Deterministic Finite Automaton (DFA) to implement the divisibility check and implement the DFA in hardware.

Creating a DFA for divisibility by 5 is easy. You just need to notice the remainders and check what 2r (mod 5) and 2r + 1(mod 5) map to. There are many websites that discuss this. For example this one.

There are well-known examples to convert DFA to a hardware representation as well.

Answer 6

How about this:

Convert the number to base 4 (this is trivial by simply combining pairs of bits). 5 in base 4 is 11. The values base 4 that are divisible by 11 are somewhat familiar: 11, 22, 33, 110, 121, 132, 203, ...

The rule for divisibility by 11 is that you add all the odd digits and all the even digits and subtract one from the other. If the result is divisible by 11 (which remember is 5), then it's divisible by 11 (which remember is 5).

For example:

123456d = 1 1110 0010 0100 0000b = 132021000_4

The even digits are 1 2 2 0 0 : sum = 5d
The odd digits are   3 0 1 0  : sum = 4d

Difference is 1, which is not divisble by 5

Or another one:

123455d = 1 1110 0010 0011 1111b = 132020333_4

The even digits are 1 2 2 3 3 : sum = 11d
The odd digits are   3 0 0 3  : sum = 6d

Difference is 5, which is a 5 or a 0

This should have a fairly efficient HW implementation because it's mostly bit-slicing, followed by N/2 adders, where N is the number of bits in the number you're interested in.

Note that after adding the digits and subtracting, the maximum value is 3/4 * N, so if you have 16-bit numbers max, you can get at most 12 as a result, so you only need to check for 0, ±5 and ±10 explicitly. If you're using 32-bit numbers then you can get at most 24 as a result, so you need to also check if the result is ±15 or ±20.