CODEWITHSUNDEEP
ccontrol-flowcyclomatic-complexityblack-boxwhite-box
AJ.
AJ.

Reputation: 2569

Control flow graph & cyclomatic complexity for following procedure

insertion_procedure (int a[], int p [], int N)
{
    int i,j,k;
    for (i=0; i<=N; i++) p[i] = i;
    for (i=2; i<=N; i++)
    {
        k = p[i];
        j = 1;
        while (a[p[j-1]] > a[k]) {p[j] = p[j-1]; j--}
        p[j] = k;
    }
}

I have to find cyclomatic complexity for this code and then suggest some white box test cases and black box test cases. But I am having trouble making a CFG for the code.

Would appreciate some help on test cases as well.

Upvotes: 11

Views: 35326

Answers (3)

Lineker
Lineker

Reputation: 335

You can also use McCabe formula M = E-N + 2C
E = edges
N = nodes
C = components
M = cyclomatic complexity

E = 14
N = 12
C = 1

M = 14-12 + 2*1 = 4

Upvotes: 2

Vincent Ramdhanie
Vincent Ramdhanie

Reputation: 103135

Start by numbering the statements:

 insertion_procedure (int a[], int p [], int N)
 {
(1)    Int i,j,k;
(2)    for ((2a)i=0; (2b)i<=N; (2c)i++) 
(3)        p[i] = i;
(4)    for ((4a)i=2; (4b)i<=N; (4c)i++)
       {
(5)       k=p[i];j=1;
(6)       while (a[p[j-1]] > a[k]) {
(7)           p[j] = p[j-1]; 
(8)           j--
          }
(9)          p[j] = k;
       }

Now you can clearly see which statement executes first and which last etc. so drawing the cfg becomes simple.

CFG

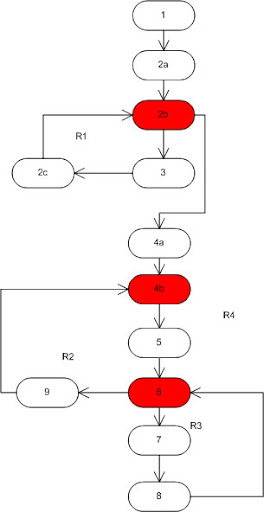
Now, to calculate cyclomatic complexity you use one of three methods:

  1. Count the number of regions on the graph: 4
  2. No. of predicates (red on graph) + 1 : 3 + 1 = 4
  3. No of edges - no. of nodes + 2: 14 - 12 + 2 = 4.

Upvotes: 28

Darin Dimitrov
Darin Dimitrov

Reputation: 1038830

The cyclomatic complexity is 4.

1 for the procedure +1 for the for loop +1 for the while loop +1 for the if condition of the while loop.

Upvotes: 3

Related Questions