CODEWITHSUNDEEP
matlabgaussian
power2
power2

Reputation: 999

Rotating a gaussian function - matlab

Good day,

I have code that stretches and rotates a gaussian 2d pdf as such:

mu = [0 0];

Sigma = [1 0; 0 1];
Scale = [3 0; 0 1];
Theta = 10;
Rotate = [cosd(Theta) -sind(Theta); sind(Theta) cosd(Theta)];
Sigma = (Sigma*Scale)*Rotate

x1 = -100:1:100; x2 = -100:1:100;
[X1,X2] = meshgrid(x1,x2);
F = mvnpdf([X1(:) X2(:)],mu,Sigma);
F = reshape(F,length(x2),length(x1));

imshow(F*255)

Unfortunately, when I change Theta to a value other than 0, it says SIGMA must be a square, symmetric, positive definite matrix. Can I know what's going on

Upvotes: 1

Views: 6416

Answers (2)

rayryeng
rayryeng

Reputation: 104535

If you consult the article on Wikipedia about the general elliptical version of the Gaussian 2D PDF, it doesn't look like you're rotating it properly. In general, the equation is:

Source: Wikipedia

where:

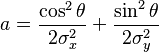
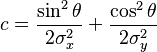
Usually, A = 1 and we'll adopt that here. The angle theta will rotate the PDF counter-clockwise, and so we can use this raw form of the equation over mvnpdf. Using your definitions and constants, it would become this:

x1 = -100:1:100; x2 = -100:1:100;
[X1,X2] = meshgrid(X1, X2);
sigma1 = 1;
sigma2 = 1;
scale1 = 3;
scale2 = 1;
sigma1 = scale1*sigma1;
sigma2 = scale2*sigma2;
Theta = 10;

a = ((cosd(Theta)^2) / (2*sigma1^2)) + ((sind(Theta)^2) / (2*sigma2^2));
b = -((sind(2*Theta)) / (4*sigma1^2)) + ((sind(2*Theta)) / (4*sigma2^2));
c = ((sind(Theta)^2) / (2*sigma1^2)) + ((cosd(Theta)^2) / (2*sigma2^2));

mu = [0 0];
A = 1;
F = A*exp(-(a*(X1 - mu(1)).^2 + 2*b*(X1 - mu(1)).*(X2 - mu(2)) + c*(X2 - mu(2)).^2));
imshow(F*255);

Upvotes: 5

Brian Goodwin
Brian Goodwin

Reputation: 391

I see that you are trying to rotate the variances in 2D... You have to hit your sigma matrix with your transform on both sides of it since the "sigma" matrix is essentially a tensor.

mu = [0 0];

Sigma = [1 0; 0 1];
Scale = [10 0;0 1];
Theta = pi/3;
m = makehgtform('zrotate',Theta);
m = m(1:2,1:2);
Sigma = m*(Sigma*Scale)*m.';

x1 = -100:1:100; 
x2 = -100:1:100;
[X1,X2] = meshgrid(x1,x2);
F = mvnpdf([X1(:) X2(:)],mu,Sigma);
F = reshape(F,length(x2),length(x1));

imshow(F*255)

Upvotes: 1

Related Questions