Wrong output while finding the root by Fixed Point Iteration

Question

I have an equation g = @(x)(5-((5/2)*exp(x/2))-((7/2).x^2)-3*x).^1/3 and, according to specs, the equation has 3 roots. But my output does not have any match between x and g(x) in order to get Fixed Points. Output:

>> fpi1(g, 0.5, 20)
   x0                                           g(x0)
  0.500000000000000                       0.670818823114861 - 1.161892284308499i
  0.670818823114861 - 1.161892284308499i  1.281297751181495 - 1.559064591427071i
  1.281297751181495 - 1.559064591427071i  1.864118571141893 - 1.621766955715062i
  1.864118571141893 - 1.621766955715062i  2.320549078066838 - 1.504496934526923i
  2.320549078066838 - 1.504496934526923i  2.646646533032701 - 1.316018792060223i
  2.646646533032701 - 1.316018792060223i  2.870437643388612 - 1.115036747500670i
  2.870437643388612 - 1.115036747500670i  3.021682102842603 - 0.927806240969038i
  3.021682102842603 - 0.927806240969038i  3.123528510261589 - 0.763760920462736i
  3.123528510261589 - 0.763760920462736i  3.192243659445853 - 0.624547007383635i
  3.192243659445853 - 0.624547007383635i  3.238827490411373 - 0.508525243060542i
  3.238827490411373 - 0.508525243060542i  3.270613725640807 - 0.412880979787002i
  3.270613725640807 - 0.412880979787002i  3.292471687008435 - 0.334576282706924i
  3.292471687008435 - 0.334576282706924i  3.307635263738642 - 0.270756021961336i
  3.307635263738642 - 0.270756021961336i  3.318257296190301 - 0.218898831715851i
  3.318257296190301 - 0.218898831715851i  3.325776161489184 - 0.176850650328430i
  3.325776161489184 - 0.176850650328430i  3.331157314339334 - 0.142806525903066i
  3.331157314339334 - 0.142806525903066i  3.335052371178708 - 0.115272146831085i
  3.335052371178708 - 0.115272146831085i  3.337903988543196 - 0.093020017690524i
  3.337903988543196 - 0.093020017690524i  3.340015124633794 - 0.075047094363536i
  3.340015124633794 - 0.075047094363536i  3.341594884710001 - 0.060536697645525i
  3.341594884710001 - 0.060536697645525i  3.342788954448884 - 0.048825574318716i

What did I do wrong? How could it be fixed?

%Program 1.2 Fixed-Point Iteration
%Computes approximate solution of g(x)=x
%Input: inline function g, starting guess x0, 
%       number of steps k
%Output: Approximate solution xc
function xc=fpi1(g,x0,k)
x(1)=x0;
for i=1:k
  x(i+1)=g(x(i));
end
xc=x(k+1);
disp('   x0                                           g(x0)');
disp([x', g(x)']);

Answer 1

Just a small note before I start. There's a typo in your g function. I'm assuming you meant (7/2)* not (7/2).. I also had to edit your code to allow the power operation to work element-wise:

g = @(x)(5-((5/2).*exp(x/2))-((7/2)*x.^2)-3*x).^1/3;

Doing some initial tests with this corrected function match up to what you're getting.

---

In any case, your use of fixed-point iterations to find the roots of an equation is incorrect. Before I go into what you need to do to fix it, I'd like to cover how fixed-point iteration works so that you (as well as everyone else who reads this post) understands where I'm coming from.

Fixed-point iterations is based on an initial input value x0. You then repeatedly calculate what the output of this value is once you submit this into a function, then reuse the output as input at the next iteration. Concretely, a fixed point iteration scheme performs this:

^{Source: Wikipedia}

Ideally, after some iterations, we would want the iterations to converge to some value x such that:

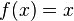
^{Source: Wikipedia}

The above is the very definition of a fixed point. To do this to find roots is not (natively) supported because finding the root of an equation contradicts what a fixed point is supposed to be. The definition of a root is when f(x) = 0 and this is not a fixed-point unless x=0. If you want to use fixed-point iterations to find the roots, then you must change the way the function f is structured. This leads us to the classical iterative root finding technique called Newton's Method which also uses fixed-point iterations to find the roots of functions, but the function f(x) is different.

I won't go into the derivation of Newton's Method, but this is what you do instead at each iteration:

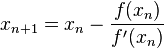
^{Source: Wikipedia}

f(x) is the function and f'(x) is the derivative of f(x). If we replaced the right hand side with a new function g(x), you would thus perform fixed-point iterations on the function g(x) and the result after convergence is the root you're looking for. Concretely, if:

^{Source: Wikipedia}

then:

^{Source: Wikipedia}

and thus:

^{Source: Wikipedia}

... and x is a root of the function f(x) if:

^{Source: Wikipedia}

Therefore, you will need to modify your code so that it doesn't take a function handle anymore. It will have to take a symbolic version because you need to take the derivative of the function.

Bearing that in mind, this is the modification you'd need to make to your code in order to get it to work:

%//Program 1.2 Fixed-Point Iteration via Newton's Method
%//Computes approximate root of g(x)=0
%//Input: symbolic function g, starting guess x0, 
%//       number of steps k
%//Output: Approximate solution xc

format long g; %// For precision
x(1)=x0;
gp = diff(g); %// Change
for i=1:k
    gval = double(subs(g, 'x', x(i))); %// Change
    gpval = double(subs(gp, 'x', x(i))); %// Change
    x(i+1)= x(i) - (gval/gpval); %// Change
end
xc=x(k+1);
y = double(subs(g, 'x', x)); %// Change
disp('                        x0                      g(x0)');
disp([x' y'])

What's different is that inside the function, you find the derivative symbolically with diff. Also, when you want to substitute values into the function, you need to use subs then cast the result to double. I'm also assuming that your function is with respect to the variable x.

The third-last line of code converts all of those x values that you accumulated into a double array for display.

To run this code, you'd do:

syms x;
g = (5-((5/2)*exp(x/2))-((7/2)*x^2)-3*x)^1/3;
xc = fpi(g, 0.5, 20);

Take note that you don't need the element-wise operators anymore, as we're dealing with symbolic equations.

We get:

>> fpi(g, 0.5, 20)
                        x0                      g(x0)
                       0.5        -0.195021180573118
         0.427814775036064       -0.0067677938874851
          0.42512303212814     -9.38738903072792e-06
         0.425119288112029     -1.81600035806892e-11
         0.425119288104786     -5.28061163184459e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17
         0.425119288104786      1.52806116318446e-17

So one of the roots is equal to 0.425119288104786. The right column tells you what the value at g(x) is evaluated at for each iteration, and you can see that it's very small... almost 0. That's the definition of a root more or less.