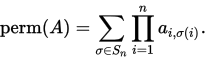Can this cython code be optimized?

Question

I am using cython for the first time to get some speed for a function. The function takes a square matrix A floating point numbers and outputs a single floating point number. The function it is computing is the permanent of a matrix

When A is 30 by 30 my code takes about 60 seconds currently on my PC.

In the code below I have implemented the Balasubramanian-Bax/Franklin-Glynn formula for the permanent from the wiki page. I have called the matrix M.

One sophisticated part of the code is the array f which is used to hold the index of the next position to flip in the array d. The array d holds values that are +-1. The manipulation of f and j in the loop is just a clever way to update a Gray code quickly.

from __future__ import division
import numpy as np
cimport numpy as np
cimport cython


DTYPE_int = np.int
ctypedef np.int_t DTYPE_int_t
DTYPE_float = np.float64
ctypedef np.float64_t DTYPE_float_t

@cython.boundscheck(False) # turn off bounds-checking for entire function
@cython.wraparound(False)  # turn off negative index wrapping for entire function
def permfunc(np.ndarray [DTYPE_float_t, ndim =2, mode='c'] M):
    cdef int n = M.shape[0]
    cdef np.ndarray[DTYPE_float_t, ndim =1, mode='c' ] d = np.ones(n, dtype=DTYPE_float)
    cdef int j =  0
    cdef int s = 1
    cdef np.ndarray [DTYPE_int_t, ndim =1, mode='c'] f = np.arange(n, dtype=DTYPE_int)
    cdef np.ndarray [DTYPE_float_t, ndim =1, mode='c'] v = M.sum(axis=0)
    cdef DTYPE_float_t p = 1
    cdef int i
    cdef DTYPE_float_t prod
    for i in range(n):
        p *= v[i]
    while (j < n-1):
        for i in range(n):
            v[i] -= 2*d[j]*M[j, i]
        d[j] = -d[j]
        s = -s
        prod = 1
        for i in range(n):
            prod *= v[i]
        p += s*prod
        f[0] = 0
        f[j] = f[j+1]
        f[j+1] = j+1
        j = f[0]
    return p/2**(n-1)   

I have used all the simple optimizations I found in the cython tutorial. Some aspects I have to admit I don't fully understand. For example, if I make the array d ints, as the values are only ever +-1, the code runs about 10% more slowly so I have left it as float64s.

Is there anything else I can do to speed up the code?

---

This is the result of cython -a . As you can see everything in the loop is compiled to C so the basic optimizations have worked.

Here is the same function in numpy which is over 100 times slower than my current cython version.

def npperm(M):
    n = M.shape[0]
    d = np.ones(n)
    j =  0
    s = 1
    f = np.arange(n)
    v = M.sum(axis=0)
    p = np.prod(v)
    while (j < n-1):
        v -= 2*d[j]*M[j]
        d[j] = -d[j]
        s = -s
        prod = np.prod(v)
        p += s*prod
        f[0] = 0
        f[j] = f[j+1]
        f[j+1] = j+1
        j = f[0]
    return p/2**(n-1)  

---

Timings updated

Here are timings (using ipython) of my cython version, the numpy version and romeric's improvement to the cython code. I have set the seed for reproducibility.

from scipy.stats import ortho_group
import pyximport; pyximport.install()
import permlib # This loads in the functions from permlib.pyx
import numpy as np; np.random.seed(7)
M = ortho_group.rvs(23) #Creates a random orthogonal matrix 
%timeit permlib.npperm(M) # The numpy version
1 loop, best of 3: 44.5 s per loop
%timeit permlib.permfunc(M) # The cython version
1 loop, best of 3: 273 ms per loop
%timeit permlib.permfunc_modified(M) #romeric's improvement
10 loops, best of 3: 198 ms per loop
M = ortho_group.rvs(28)
%timeit permlib.permfunc(M) # The cython version run on a 28x28 matrix
1 loop, best of 3: 15.8 s per loop
%timeit permlib.permfunc_modified(M) # romeric's improvement run on a 28x28 matrix
1 loop, best of 3: 12.4 s per loop

Can the cython code be sped up at all?

I am using gcc and the CPU is the AMD FX 8350.

Answer 1

Disclaimer: I'm the core dev of the tool mentioned below.

As an alternative to Cython, you can give Pythran a try. A single annotation to the original NumPy code:

#pythran export npperm(float[:, :])
import numpy as np
def npperm(M):
    n = M.shape[0]
    d = np.ones(n)
    j =  0
    s = 1
    f = np.arange(n)
    v = M.sum(axis=0)
    p = np.prod(v)
    while j < n-1:
        v -= 2*d[j]*M[j]
        d[j] = -d[j]
        s = -s
        prod = np.prod(v)
        p += s*prod
        f[0] = 0
        f[j] = f[j+1]
        f[j+1] = j+1
        j = f[0]
    return p/2**(n-1)

compiled with:

> pythran perm.py

yields a speedup similar to the one with Cython:

> # numpy version
> python -mtimeit -r3 -n1 -s 'from scipy.stats import ortho_group; from perm import npperm; import numpy as np; np.random.seed(7); M = ortho_group.rvs(23)' 'npperm(M)'
1 loops, best of 3: 21.7 sec per loop
> # pythran version
> pythran perm.py
> python -mtimeit -r3 -n1 -s 'from scipy.stats import ortho_group; from perm import npperm; import numpy as np; np.random.seed(7); M = ortho_group.rvs(23)' 'npperm(M)' 
1 loops, best of 3: 171 msec per loop

with no need to reimplement sum_axis (Pythran takes care of that).

More interesting, Pythran is capable of recognizing several vectorizable (in the sense of generating SSE/AVX intrinsics) patterns, through an option flag:

> pythran perm.py -DUSE_BOOST_SIMD -march=native
>  python -mtimeit -r3 -n10 -s 'from scipy.stats import ortho_group; from perm import npperm; import numpy as np; np.random.seed(7); M = ortho_group.rvs(23)' 'npperm(M)' 
10 loops, best of 3: 93.2 msec per loop

which makes a final x232 speedup with respect to the NumPy version, a speedup comparable to the unrolled Cython version, without much manual tuning.

Answer 2

This answer is based on the code of @romeric posted before. I corrected the code and simplified it, and added the cdivisioncompiler directive.

@cython.boundscheck(False) 
@cython.wraparound(False)
@cython.cdivision(True)
def permfunc_modified_2(np.ndarray [double, ndim =2, mode='c'] M):
    cdef:
        int n = M.shape[0], s=1, i, j
        int *f = <int*>malloc(n*sizeof(int))
        double *d = <double*>malloc(n*sizeof(double))
        double *v = <double*>malloc(n*sizeof(double))
        double p = 1, prod

    for i in range(n):
        v[i] = 0.
        for j in range(n):
            v[i] += M[j,i]
        p *= v[i]
        f[i] = i
        d[i] = 1
    j = 0
    while (j < n-1):
        prod = 1.
        for i in range(n):
            v[i] -= 2.*d[j]*M[j, i]
            prod *= v[i]
        d[j] = -d[j]
        s = -s            
        p += s*prod
        f[0] = 0
        f[j] = f[j+1]
        f[j+1] = j+1
        j = f[0]

    free(d)
    free(f)
    free(v)
    return p/pow(2.,(n-1))

The original code of @romeric didn't initialize v, so you get different results sometimes. Additionally, I combined the two loops before the while and the two loops inside of the while respectively.

Finally, the comparison

In [1]: from scipy.stats import ortho_group
In [2]: import permlib
In [3]: import numpy as np; np.random.seed(7)
In [4]: M = ortho_group.rvs(5)
In [5]: np.equal(permlib.permfunc(M), permlib.permfunc_modified_2(M))
Out[5]: True
In [6]: %timeit permfunc(M)
10000 loops, best of 3: 20.5 µs per loop
In [7]: %timeit permlib.permfunc_modified_2(M)
1000000 loops, best of 3: 1.21 µs per loop
In [8]: M = ortho_group.rvs(15)
In [9]: np.equal(permlib.permfunc(M), permlib.permfunc_modified_2(M))
Out[9]: True
In [10]: %timeit permlib.permfunc(M)
1000 loops, best of 3: 1.03 ms per loop
In [11]: %timeit permlib.permfunc_modified_2(M)
1000 loops, best of 3: 432 µs per loop
In [12]: M = ortho_group.rvs(28)
In [13]: np.equal(permlib.permfunc(M), permlib.permfunc_modified_2(M))
Out[13]: True
In [14]: %timeit permlib.permfunc(M)
1 loop, best of 3: 14 s per loop
In [15]: %timeit permlib.permfunc_modified_2(M)
1 loop, best of 3: 5.73 s per loop

Answer 3

There isn't much you can do with your cython function, as it is already well optimised. However, you will still be able to get a moderate speed-up by completely avoiding the calls to numpy.

import numpy as np
cimport numpy as np
cimport cython
from libc.stdlib cimport malloc, free
from libc.math cimport pow

cdef inline double sum_axis(double *v, double *M, int n):
    cdef:
        int i, j
    for i in range(n):
        for j in range(n):
            v[i] += M[j*n+i]


@cython.boundscheck(False) 
@cython.wraparound(False)
def permfunc_modified(np.ndarray [double, ndim =2, mode='c'] M):
    cdef:
        int n = M.shape[0], j=0, s=1, i
        int *f = <int*>malloc(n*sizeof(int))
        double *d = <double*>malloc(n*sizeof(double))
        double *v = <double*>malloc(n*sizeof(double))
        double p = 1, prod

    sum_axis(v,&M[0,0],n)

    for i in range(n):
        p *= v[i]
        f[i] = i
        d[i] = 1

    while (j < n-1):
        for i in range(n):
            v[i] -= 2.*d[j]*M[j, i]
        d[j] = -d[j]
        s = -s
        prod = 1
        for i in range(n):
            prod *= v[i]
        p += s*prod
        f[0] = 0
        f[j] = f[j+1]
        f[j+1] = j+1
        j = f[0]

    free(d)
    free(f)
    free(v)
    return p/pow(2.,(n-1)) 

Here are essential checks and timings:

In [1]: n = 12
In [2]: M = np.random.rand(n,n)
In [3]: np.allclose(permfunc_modified(M),permfunc(M))
True
In [4]: n = 28
In [5]: M = np.random.rand(n,n)
In [6]: %timeit permfunc(M) # your version
1 loop, best of 3: 28.9 s per loop
In [7]: %timeit permfunc_modified(M) # modified version posted above
1 loop, best of 3: 21.4 s per loop

EDIT Lets perform some basic SSE vectorisation by unrolling the inner prod loop, that is change the loop in the above code to the following

# define t1, t2 and t3 earlier as doubles
t1,t2,t3=1.,1.,1.
for i in range(0,n-1,2):
    t1 *= v[i]
    t2 *= v[i+1]
# define k earlier as int
for k in range(i+2,n):
    t3 *= v[k]
p += s*(t1*t2*t3) 

and now the timing

In [8]: %timeit permfunc_modified_vec(M) # vectorised
1 loop, best of 3: 14.0 s per loop

So almost 2X speed-up over the original optimised cython code, not bad.

Answer 4

Well, one obvious optimization is to set d[i] to -2 and +2 and avoid the multiplication by 2. I suspect this won't make any difference, but still.

Another is to make sure the C++ compiler that compiles the resulting code has all the optimizations turned on (especially vectorization).

The loop that calculates the new v[i]s can be parallelized with Cython's support of OpenMP. At 30 iterations this also might not make a difference.