Reputation: 516
A maze generation algorithm where I can choose entrance and exit points
What would be a good maze generation algorithm where the developer can choose entrance and exit points arbitrarily (both of them should be located on the edges, of course)? A piece of pseudocode or an implementation in any language would be most helpful.
Upvotes: 0
Views: 3716
Answers (3)
Reputation: 121
For an implementation that generates a random maze from any planar graph, check out this web app. For a slightly different take on it, and a general description of dual graphs, I've also put together a presentation.
Note, the notion of an entry or exit is something I have not addressed at all. But, given a well defined maze, you can always place the entry and exit points at any location. (Granted, some may lead to trivial traversals as the solution.) In any maze, you should always be able to travel between any two points or 'rooms'.
Finding an entry and exit point that results in an interesting or sufficiently complex solution given a particular maze is likely just a matter of ensuring a solution with a sufficient length. If you'd like to pre-specify an entry an exit point for an arbitrary graph, that can also be done pretty simply.
If you have a graph and want to add a start or end point, all you need to do is add a 'room' to the perimeter. This room has to be reachable to the rest of the maze, and it can only be reached by removing the wall between it and the rest of the maze. The idea is shown in the following, with the start and end rooms as the triangles at the top left and bottom right:
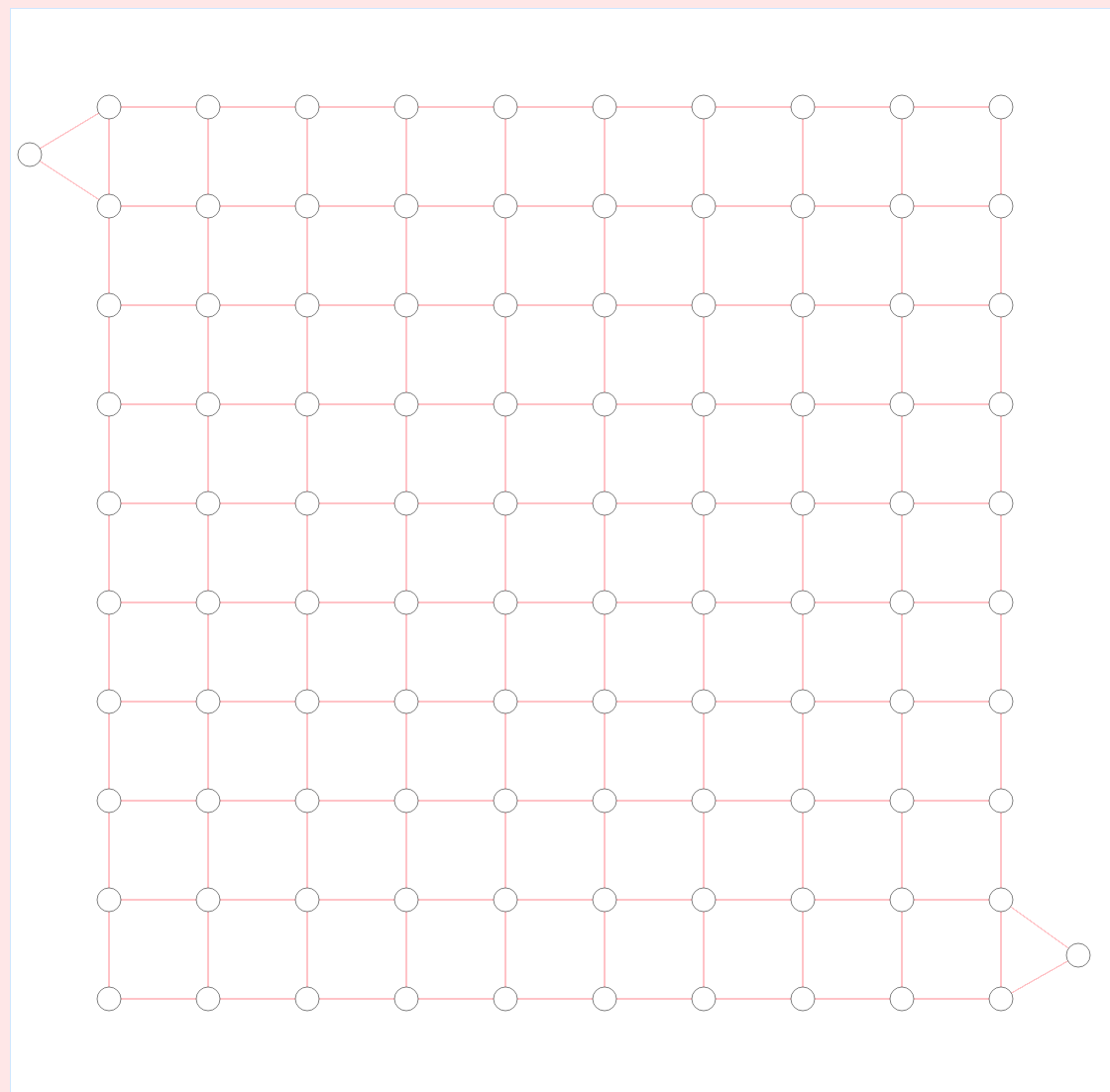 .
.
A random maze from the graph would be as follows:
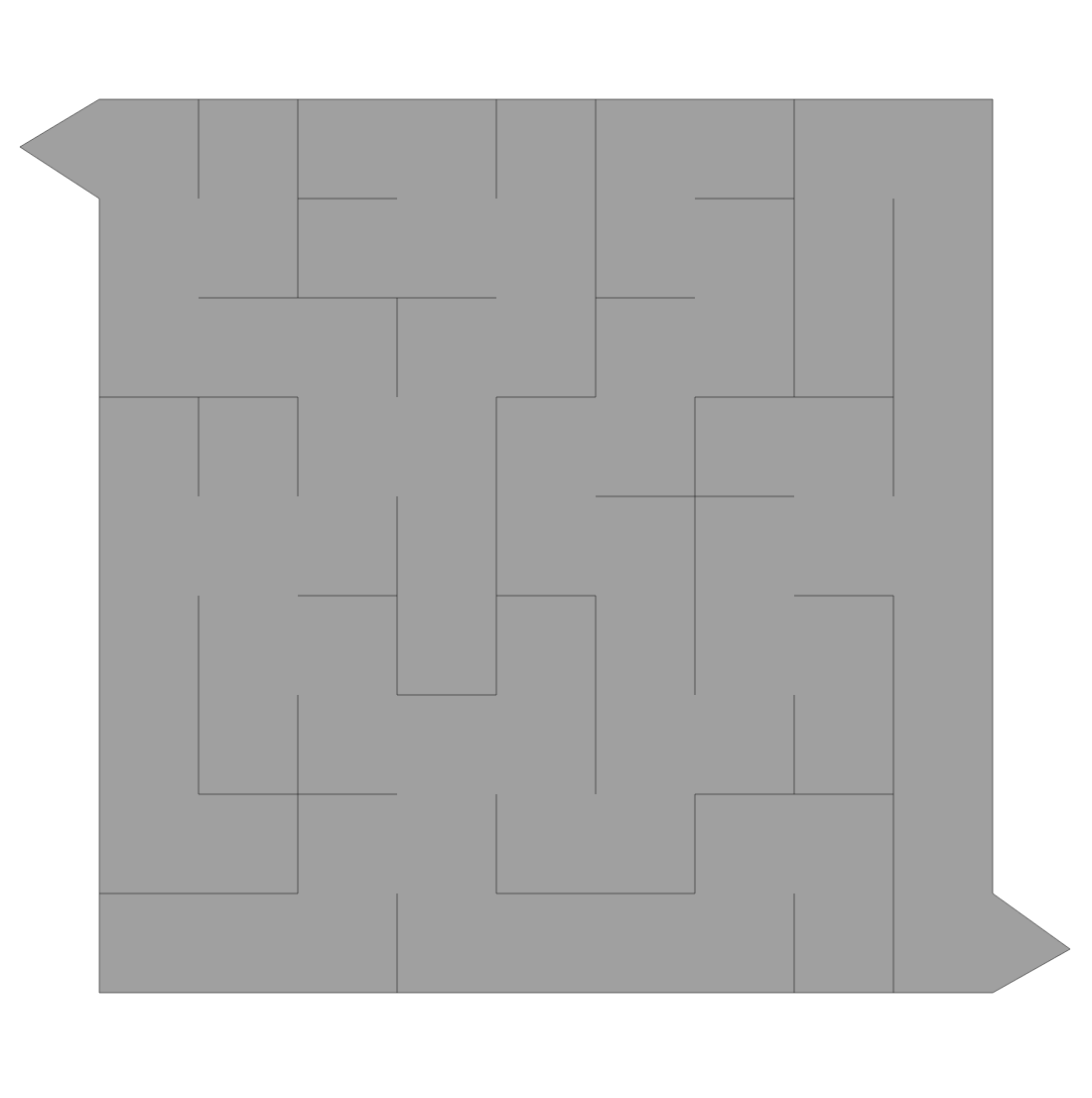
Upvotes: 0
Reputation: 50017
There are many algorithms for generating mazes: with a little work I expect you can change them to allow the starting and ending points to be specified.
The best reference I'm aware of for mazes is Mazes For Programmers by Jamis Buck. Jamis blogs about many things software-related, and among his posts you can find quite a few on maze algorithms. The following is a recap of what's on his blog:
-
- Initialize the cells of the first row to each exist in their own set.
- Now, randomly join adjacent cells, but only if they are not in the same set. When joining adjacent cells, merge the cells of both sets into a single set, indicating that all cells in both sets are now connected (there is a path that connects any two cells in the set).
- For each set, randomly create vertical connections downward to the next row. Each remaining set must have at least one vertical connection. The cells in the next row thus connected must share the set of the cell above them.
- Flesh out the next row by putting any remaining cells into their own sets.
- Repeat until the last row is reached.
- For the last row, join all adjacent cells that do not share a set, and omit the vertical connections, and you’re done!
-
- Throw all of the edges in the graph into a big burlap sack. (Or, you know, a set or something.)
- Pull out the edge with the lowest weight. If the edge connects two disjoint trees, join the trees. Otherwise, throw that edge away.
- Repeat until there are no more edges left.
-
- Choose an arbitrary vertex from G (the graph), and add it to some (initially empty) set V.
- Choose the edge with the smallest weight from G, that connects a vertex in V with another vertex not in V.
- Add that edge to the minimal spanning tree, and the edge’s other vertex to V.
- Repeat steps 2 and 3 until V includes every vertex in G.
-
- Begin with an empty field.
- Bisect the field with a wall, either horizontally or vertically. Add a single passage through the wall.
- Repeat step #2 with the areas on either side of the wall.
- Continue, recursively, until the maze reaches the desired resolution.
-
- Choose a starting point in the field.
- Randomly choose a wall at that point and carve a passage through to the adjacent cell, but only if the adjacent cell has not been visited yet. This becomes the new current cell.
- If all adjacent cells have been visited, back up to the last cell that has uncarved walls and repeat.
- The algorithm ends when the process has backed all the way up to the starting point.
-
- Choose a vertex. Any vertex.
- Choose a connected neighbor of the vertex and travel to it. If the neighbor has not yet been visited, add the traveled edge to the spanning tree.
- Repeat step 2 until all vertexes have been visited.
-
- Choose any vertex at random and add it to the UST.
- Select any vertex that is not already in the UST and perform a random walk until you encounter a vertex that is in the UST.
- Add the vertices and edges touched in the random walk to the UST.
- Repeat 2 and 3 until all vertices have been added to the UST.
-
- Choose a starting location.
- Perform a random walk, carving passages to unvisited neighbors, until the current cell has no unvisited neighbors.
- Enter “hunt” mode, where you scan the grid looking for an unvisited cell that is adjacent to a visited cell. If found, carve a passage between the two and let the formerly unvisited cell be the new starting location.
- Repeat steps 2 and 3 until the hunt mode scans the entire grid and finds no unvisited cells.
-
- Let C be a list of cells, initially empty. Add one cell to C, at random.
- Choose a cell from C, and carve a passage to any unvisited neighbor of that cell, adding that neighbor to C as well. If there are no unvisited neighbors, remove the cell from C.
- Repeat #2 until C is empty.
-
- For every cell in the grid, randomly carve a passage either north, or west.
- Yes, that's it.
-
- Work through the grid row-wise, starting with the cell at 0,0. Initialize the “run” set to be empty.
- Add the current cell to the “run” set.
- For the current cell, randomly decide whether to carve east or not.
- If a passage was carved, make the new cell the current cell and repeat steps 2-4.
- If a passage was not carved, choose any one of the cells in the run set and carve a passage north. Then empty the run set, set the next cell in the row to be the current cell, and repeat steps 2-5.
- Continue until all rows have been processed.
Best of luck.
Upvotes: 3

Reputation: 514
While not exactly an algorithm, i describe here some steps in creating a maze. Each of these steps will need to be turned into code, but i think they are a good starting point.
step 0: Initially, all the squares in the matrix have all their borders marked as walls.

Later on, some of these walls will be cut, such as to create paths.
In the following image, every wall that will be intersected by a path will be cut;
all the walls that are not cut by any path will be kept.
step 1: We start the following way: create the most simple path between the entry and the exit points; this path will be made of only one horizontal and one vertical line.
Next, because this path is too simple, we try to make it more complicated (more twisted, having more turns); we do this by gradually replacing segments of the existing path, with three sides of a rectangle (which, together with the removed segment, would have represented an entire rectangle); we repeat this step as many times as necessary, only taking care that the path will not intersect itself.
step 2: Now we have a relatively complicated path that connects the entry and exit points in the maze. However, there are still cells in the matrix will walls surrounding them on all 4 sides. I have looked for some examples of mazes, and i have noticed that every cell in the maze is potentially accessible from the entry point, even though it is a dead end. (to put it in another way, all the paths in the maze form a tree).
What we need to do now is to connect all the remaining cells in the maze to the existing path. As a convention, i will call 'main path' the path that we have just created from the entry to the exit points; all the other paths that branch out of it will be named 'secondary paths'. So how do we create secondary paths? By picking one random point in the large areas of the maze that are not traversed by the main path, and another random point on the main path. Than link these points in a similar way that we did with the entry and exit points: link them with the most simple path possible, later make this path more complicated - by replacing a segment with the 3 segments that would make the complement of a rectangle. We won't need to repeat this step many times because the secondary paths don't need to be more complicated than the main path.
step 3: Now we have created several secondary paths , by linking some random points in the maze with the main path. There are still some areas that are inaccessible, but they are small. So for these cells, we can just link them with a straight line to the nearest point in either the main path or a secondary path, and that's it. All the squares in the maze are accessible. All we need to do now is to remove any wall that is intersected by a path, and keep all the other walls.
Upvotes: 2
Related Questions
- Algorithm for traversing a maze
- Algorithm for maze/labyrinth generation with no dead ends?
- Infinite maze generating algorithm
- Algorithm to get through a maze
- Best algorithm for maze solving?
- How to generate a maze with more than one successful path?
- Generating and solving a maze with no boundaries?
- Algorithm to generate a maze with / without solution
- Efficient algorithm to generate a kind of maze
- Maze solving algorithm. Complex mazes


