CODEWITHSUNDEEP
haskell
w41g87
w41g87

Reputation: 79

Using non-fractional complex number in Haskell

When using the native Data.Complex implementation in Haskell, constructing a complex number using non-fractional type using Int is possible. However, it is impossible to perform any calculation with it:

> let x = 1:+1 :: Complex Int
> x * x

<interactive>:44:1: error:
    * No instance for (RealFloat Int) arising from a use of `*'
    * In the expression: x * x
      In an equation for `it': it = x * x

This becomes a problem when I am trying to use arbitrary significance structures like Data.Scientific since it has no instance for RealFloat as well. What can I do to remedy this situation? Writing an instance of RealFloat for Scientifc will result in an orphan instance. Should I write my own Complex class?

Upvotes: 2

Views: 93

Answers (1)

willeM_ Van Onsem
willeM_ Van Onsem

Reputation: 476709

In order to perform functions defined in the Num typeclass, the item a of Complex a should be a member of the RealFloat typeclass. Indeed, the source code shows us:

-- | @since 2.01
instance  (RealFloat a) => Num (Complex a)  where
    -- …
    signum (0:+0)       =  0
    signum z@(x:+y)     =  x/r :+ y/r  where r = magnitude z

Here the signum is the culprit, since this returns x /r + y i / r with r the magnitude of the complex number. It basically normalizes the complex number to coordinates on a unit circle:

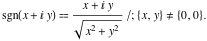
the sign of a complex number is the complex number divided by the magnitude of complex number.

We determine the magnitude of a complex number with [src]:

magnitude :: (RealFloat a) => Complex a -> a
magnitude (x:+y) =  scaleFloat k
                     (sqrt (sqr (scaleFloat mk x) + sqr (scaleFloat mk y)))
                    where k  = max (exponent x) (exponent y)
                          mk = - k
                          sqr z = z * z

Here the exponent :: RealFloat a => a -> Int, this thus requires a to ben an instance of the RealFloat typeclass.

Since Num defines several methods, it is sufficient that one of these methods has a type constraint, to enforce these constraint on the Num class, and thus all the methods are defined in the Num instance.

Writing an instance of RealFloat for Scientifc will result in an orphan instance.

You can make use of the toRealFloat :: RealFloat a => Scientific -> a. We thus can work with:

Prelude Data.Scientific Data.Complex> let x = 1 :+ 1 :: Complex Scientific
Prelude Data.Scientific Data.Complex> let x' = toRealFloat <$> x
Prelude Data.Scientific Data.Complex> x' * x'
0.0 :+ 2.0

Upvotes: 1

Related Questions