CODEWITHSUNDEEP
image-processingconvolution
user280407
user280407

Reputation:

Convolution theory vs implementation

I study convolution in image processing as it is a part of the curriculum, I understand the theory and the formula but I am confused about its implementation.

The formula is:

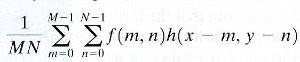
enter image description here

What I understand

The convolution kernel is flipped both horizontally and vertically then the values in the kernel are multiplied by the corresponding pixel values, the results are summed, divided by "row x column" to get the average, and then finally this result is the value of the pixel at the center of the kernel location.

Confusion in implementation

When I run the example convolution program from my course material and insert as input a 3x3 convolution kernel where:

1st row: (0, 1, 0)

2nd row: (0, 0, 0)

3rd row: (0, 0, 0)

The processed image is shifted down by one pixel, where I expected it to shift upwards by one pixel. This result indicates that no horizontal or vertical flipping is done before calculating (as if it is doing correlation).

I thought there might be a fault in the program so I looked around and found that Adobe Flex 3 and Gimp are doing this as well.

I don't understand, is there something that I missed to notice?

Appreciate any help or feedback.

Upvotes: 3

Views: 1555

Answers (2)

Niki
Niki

Reputation: 15867

I guess the programs you tried implement correlation instead of convolution.

I've tried your filter in Mathematica using the ImageFilter function, the result is shifted upwards as expected:

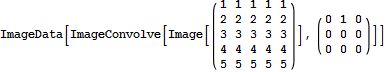
enter image description here

result:

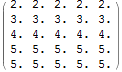
enter image description here

I've also tried it in Octave (an open source Matlab clone):

imfilter([1,1,1,1,1;
          2,2,2,2,2;
          3,3,3,3,3;
          4,4,4,4,4;
          5,5,5,5,5],
         [0,1,0;
          0,0,0;
          0,0,0],"conv")

("conv" means convolution - imfilter's default is correlation). Result:

   2   2   2   2   2
   3   3   3   3   3
   4   4   4   4   4
   5   5   5   5   5
   0   0   0   0   0

Note that the last row is different. That's because different implementations use different padding (by default). Mathematica uses constant padding for ImageConvolve, no padding for ListConvolve. Octave's imfilter uses zero padding.

Also note that (as belisarius mentioned) the result of a convolution can be smaller, same size or larger than the source image. (I've read the terms "valid", "same size" and "full" convolution in the Matlab and IPPI documentation, but I'm not sure if that's standard terminology). The idea is that the summation can either be performed

  • only over the source image pixels where the kernel is completely inside the image. In that case, the result is smaller than the source image.
  • over every source pixel. In that case, the result has the same size as the source image. This requires padding at the borders
  • over every pixel where any part of the kernel is inside the source image. In that case, the result image is larger than the source image. This also requires padding at the borders.

Upvotes: 4

Dr. belisarius
Dr. belisarius

Reputation: 61056

Please note that:

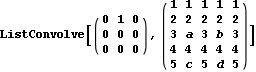
enter image description here

Results in:

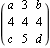
enter image description here

So, the "shifting" is not real, as the dimensions are affected.

Upvotes: 0

Related Questions