CODEWITHSUNDEEP
algorithmlanguage-agnosticcomparison
user54579
user54579

Reputation: 4688

Sorted list difference

I have the following problem.

I have a set of elements that I can sort by a certain algorithm A . The sorting is good, but very expensive.

There is also an algorithm B that can approximate the result of A. It is much faster, but the ordering will not be exactly the same.

Taking the output of A as a 'golden standard' I need to get a meaningful estimate of the error resulting of the use of B on the same data.

Could anyone please suggest any resource I could look at to solve my problem? Thanks in advance!

EDIT :

As requested : adding an example to illustrate the case : if the data are the first 10 letters of the alphabet,

A outputs : a,b,c,d,e,f,g,h,i,j

B outputs : a,b,d,c,e,g,h,f,j,i

What are the possible measures of the resulting error, that would allow me to tune the internal parameters of algorithm B to get result closer to the output of A?

Upvotes: 8

Views: 2588

Answers (7)

E.loic
E.loic

Reputation: 1

if anyone is using R language, I've implemented a function that computes the "spearman rank correlation coefficient" using the method described above by @bubake :

get_spearman_coef <- function(objectA, objectB) {
  #getting the spearman rho rank test 
  spearman_data <- data.frame(listA = objectA, listB = objectB)
  spearman_data$rankA <- 1:nrow(spearman_data) 
  rankB <- c()
  
  for (index_valueA in 1:nrow(spearman_data)) {
    for (index_valueB in 1:nrow(spearman_data)) {
      
      if (spearman_data$listA[index_valueA] == spearman_data$listB[index_valueB]) {
        rankB <- append(rankB, index_valueB)
      }
      
      
    }
  }
  spearman_data$rankB <- rankB
  spearman_data$distance <-(spearman_data$rankA - spearman_data$rankB)**2
  
  spearman <- 1 - ( (6 * sum(spearman_data$distance)) / (nrow(spearman_data) * ( nrow(spearman_data)**2 -1) ) )
  print(paste("spearman's rank correlation coefficient"))
  return( spearman)  
}

results :

get_spearman_coef(c("a","b","c","d","e"), c("a","b","c","d","e"))

spearman's rank correlation coefficient: 1

get_spearman_coef(c("a","b","c","d","e"), c("b","a","d","c","e"))

spearman's rank correlation coefficient: 0.9

Upvotes: 0

bubaker
bubaker

Reputation: 2289

Spearman's rho

I think what you want is Spearman's rank correlation coefficient. Using the index [rank] vectors for the two sortings (perfect A and approximate B), you calculate the rank correlation rho ranging from -1 (completely different) to 1 (exactly the same):

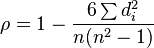
Spearman's rho

where d(i) are the difference in ranks for each character between A and B

You can defined your measure of error as a distance D := (1-rho)/2.

Upvotes: 6

Pratik Deoghare
Pratik Deoghare

Reputation: 37172

Calculating RMS Error may be one of the many possible methods. Here is small python code.

def calc_error(out_A,out_B):
        # in    <= input
        # out_A <= output of algorithm A
        # out_B <= output of algorithm B

        rms_error = 0

        for i in range(len(out_A)):
            # Take square of differences and add
            rms_error +=  (out_A[i]-out_B[i])**2 

        return rms_error**0.5   # Take square root

>>> calc_error([1,2,3,4,5,6],[1,2,3,4,5,6])
0.0
>>> calc_error([1,2,3,4,5,6],[1,2,4,3,5,6]) # 4,3 swapped
1.414
>>> calc_error([1,2,3,4,5,6],[1,2,4,6,3,5]) # 3,4,5,6 randomized
2.44

NOTE: Taking square root is not necessary but taking squares is as just differences may sum to zero. I think that calc_error function gives approximate number of wrongly placed pairs but I dont have any programming tools handy so :(.

Take a look at this question.

Upvotes: 2

benjismith
benjismith

Reputation: 16735

It's tough to give a good generic answer, because the right solution for you will depend on your application.

One of my favorite options is just the number of in-order element pairs, divided by the total number of pairs. This is a nice, simple, easy-to-compute metric that just tells you how many mistakes there are. But it doesn't make any attempt to quantify the magnitude of those mistakes.

double sortQuality = 1;
if (array.length > 1) {
   int inOrderPairCount = 0;
   for (int i = 1; i < array.length; i++) {
      if (array[i] >= array[i - 1]) ++inOrderPairCount;
   }
   sortQuality = (double) inOrderPairCount / (array.length - 1);
}

Upvotes: 2

Daniel Br&#252;ckner
Daniel Br&#252;ckner

Reputation: 59675

I would determine the largest correctly ordered sub set.

                               +-------------> I
                               |   +--------->
                               |   |
A -> B -> D ----->  E  -> G -> H --|--> J
     |             ^ |             |    ^
     |             | |             |    |
     +------> C ---+ +-----------> F ---+

In your example 7 out of 10 so the algorithm scores 0.7. The other sets have the length 6. Correct ordering scores 1.0, reverse ordering 1/n.

I assume that this is related to the number of inversions. x + y indicates x <= y (correct order) and x - y indicates x > y (wrong order).

A + B + D - C + E + G + H - F + J - I

We obtain almost the same result - 6 of 9 are correct scorring 0.667. Again correct ordering scores 1.0 and reverse ordering 0.0 and this might be much easier to calculate.

Upvotes: 4

Ed Marty
Ed Marty

Reputation: 39700

Are you looking for finding some algorithm that calculates the difference based on array sorted with A and array sorted with B as inputs? Or are you looking for a generic method of determining on average how off an array would be when sorted with B?

If the first, then I suggest something as simple as the distance each item is from where it should be (an average would do better than a sum to remove length of array as an issue)

If the second, then I think I'd need to see more about these algorithms.

Upvotes: 3

z -
z -

Reputation: 7178

you could try something involving hamming distance

Upvotes: 1

Related Questions