CODEWITHSUNDEEP
actionscript-3mathprojectiongame-physics
Fabricio
Fabricio

Reputation: 7925

Shooting projectiles given an angle and power

I'm doing a prototype game like Worms and I would like not only to shot, but also see the whole projection curve where my shot will travel before it hit the ground. The only information given by the player is an angle and a power. There is also some level elements like wind and gravity.

Can I have a code for the projection curve? its like a parabola I think. I research about parabola but I had some difficult to apply these math formulas into the programming code.

Thanks.

Upvotes: 0

Views: 2021

Answers (1)

pho
pho

Reputation: 25489

The math (and physics) part

So this seems like 10th grade physics to me.

The path trced by a projectile is (as you said) a parbola describable by the equation

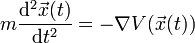
Projectile differential equation

Now, if you solve this equation, you get the following parameters:

Range: Range of projectile

Height: Height of projectile

(vi = initial velocity, theta i = initial angle of shooting wrt horizontal)

And, the equation in (x, y) for the parabolic path will be

Prabola path equation

(v0 = initial velocity, theta = firing angle)

The programming part

assuming the following constants:

const g:Number = 9.81; //9.81 m/s, the grav const

The sin function is available as Math.sin

The power function is available as Math.pow. This means, sine squared will be 

Math.pow(Math.sin(theta), 2)

You could write the range function as

function projectileRange(vel:Number, angle:Number):Number {
    var vsquare:Number = vel * vel;
    var rv:Number = vsquare * Math.sin(2 * angle) / g;
    return rv;
}

and the height function as

function projectileHeight(vel:Number, angle:Number):Number {
    var vsquare:Number = vel * vel;
    var rv:Number = vsquare * Math.pow(Math.sin(angle), 2) / (2 * g);
    return rv;
}

and the yPosition function as

function yPosition(xPos:Number, vel:Number, angle:Number):Number {
    return xPos * Math.tan(angle) - (g * xPos * xPos / (2 * vel * vel * Math.cos(angle) * Math.cos(angle)));
}

Note that the angles are in RADIANS

function toRadians(degrees:Number):void {
    return degrees * Math.PI / 180;
}

For more information on projectile motion, google it.

Upvotes: 4

Related Questions