Reputation: 14074

How can I tell if a point belongs to a certain line?

Examples are appreciated, if possible.

Upvotes: 20

Answers (10)

Eclipse

Reputation: 45493

In the simplest form, just plug the coordinates into the line equation and check for equality.

Given:

Point p (X=4, Y=5)
Line l (Slope=1, YIntersect=1)

Plug in X and Y:

   Y = Slope * X + YIntersect
=> 5 = 1 * 4 + 1
=> 5 = 5

So yes, the point is on the line.

If your lines are represented in (X1,Y1),(X2,Y2) form, then you can calculate slope with:

 Slope = (y1 - y2) / (x1-x2)

And then get the Y-Intersect with this:

 YIntersect = - Slope * X1 + Y1;

Edit: I fixed the Y-Intersect (which has been X1 / Y1 ...)

You'll have to check that x1 - x2 is not 0. If it is, then checking if the point is on the line is a simple matter of checking if the Y value in your point is equal to either x1 or x2. Also, check that the X of the point is not 'x1' or 'x2'.

Upvotes: 30

IAbstract

Reputation: 19871

As an alternative to the slope/y-intercept method, I chose this approach using Math.Atan2:

// as an extension method
public static bool Intersects(this Vector2 v, LineSegment s) {
    //  check from line segment start perspective
    var reference = Math.Atan2(s.Start.Y - s.End.Y, s.Start.X - s.End.X);
    var aTanTest = Math.Atan2(s.Start.Y - v.Y, s.Start.X - v.X);

    //  check from line segment end perspective
    if (reference == aTanTest) {
        reference = Math.Atan2(s.End.Y - s.Start.Y, s.End.X - s.Start.X);
        aTanTest = Math.Atan2(s.End.Y - v.Y, s.End.X - v.X);
    }

    return reference == aTanTest;
}

The first check reference determines the arcTan from the start point of the line segment to it's end-point. Then from the start point perspective, we determine the arcTan to the vector v.

If those values are equal, we check from the perspective of the end-point.

Simple and handles horizontal, vertical and all else in between.

Upvotes: 0

Daniel Brückner

Reputation: 59645

Given two points on the line L0 and L1 and the point to test P.

               (L1 - L0) * (P - L0)
n = (P - L0) - --------------------- (L1 - L0)
               (L1 - L0) * (L1 - L0)

The norm of the vector n is the distance of the point P from the line through L0 and L1. If this distance is zero or small enough (in the case of rounding errors), the point lies on the line.

The symbol * represents the dot product.

Example

P = (5, 5)

L0 = (0, 10)
L1 = (20, -10)

L1 - L0 = (20, -20)
P  - L0 = (5, -5)

              (20, -20) * (5, -5)
n = (5, -5) - --------------------- (20, -20)
              (20, -20) * (20, -20)

              200
  = (5, -5) - --- (20, -20)
              800

  = (5, -5) - (5, -5)

  = (0, 0)

Upvotes: 7

Robin Andersson

Reputation: 5370

I just wrote an function which handles a few extra requirements since I use this check in a drawing application:

Fuzziness - There must be some room for error since the function is used to select lines by clicking on them.
The line got an EndPoint and a StartPoint, no infinite lines.
Must handle straight vertical and horizontal lines, (x2 - x1) == 0 causes division by zero in the other answers.

private const double SELECTION_FUZZINESS = 3;

internal override bool ContainsPoint(Point point)
{
    LineGeometry lineGeo = geometry as LineGeometry;
    Point leftPoint;
    Point rightPoint;

    // Normalize start/end to left right to make the offset calc simpler.
    if (lineGeo.StartPoint.X <= lineGeo.EndPoint.X)
    {
        leftPoint   = lineGeo.StartPoint;
        rightPoint  = lineGeo.EndPoint;
    }
    else
    {
        leftPoint   = lineGeo.EndPoint;
        rightPoint  = lineGeo.StartPoint;
    }

    // If point is out of bounds, no need to do further checks.                  
    if (point.X + SELECTION_FUZZINESS < leftPoint.X || rightPoint.X < point.X - SELECTION_FUZZINESS)
        return false;
    else if (point.Y + SELECTION_FUZZINESS < Math.Min(leftPoint.Y, rightPoint.Y) || Math.Max(leftPoint.Y, rightPoint.Y) < point.Y - SELECTION_FUZZINESS)
        return false;

    double deltaX = rightPoint.X - leftPoint.X;
    double deltaY = rightPoint.Y - leftPoint.Y;

    // If the line is straight, the earlier boundary check is enough to determine that the point is on the line.
    // Also prevents division by zero exceptions.
    if (deltaX == 0 || deltaY == 0) 
        return true;

    double slope        = deltaY / deltaX;
    double offset       = leftPoint.Y - leftPoint.X * slope;
    double calculatedY  = point.X * slope + offset;

    // Check calculated Y matches the points Y coord with some easing.
    bool lineContains = point.Y - SELECTION_FUZZINESS <= calculatedY && calculatedY <= point.Y + SELECTION_FUZZINESS;

    return lineContains;            
}

Upvotes: 28

Patrick McDonald

Reputation: 65411

If you have a line defined by its endpoints

PointF pt1, pt2;

and you have a point that you want to check

PointF checkPoint;

then you could define a function as follows:

bool IsOnLine(PointF endPoint1, PointF endPoint2, PointF checkPoint) 
{
    return (checkPoint.Y - endPoint1.Y) / (endPoint2.Y - endPoint1.Y)
        == (checkPoint.X - endPoint1.X) / (endPoint2.X - endPoint1.X);
}

and call it as follows:

if (IsOnLine(pt1, pt2, checkPoint) {
    // Is on line
}

You will need to check for division by zero though.

Upvotes: 3

Wahid Bitar

Reputation: 14074

I think Mr.Patrick McDonald put the nearly correct answer and this is the correction of his answer:

public bool IsOnLine(Point endPoint1, Point endPoint2, Point checkPoint)
{
    return (((double)checkPoint.Y - endPoint1.Y)) / ((double)(checkPoint.X - endPoint1.X))
        == ((double)(endPoint2.Y - endPoint1.Y)) / ((double)(endPoint2.X - endPoint1.X));
}

and of course there are many other correct answers especially Mr.Josh but i found this is the best one.

Thankx for evryone.

Upvotes: 6

Dave

Reputation: 10577

The best way to determine if a point R = (rx, ry) lies on the line connecting points P = (px, py) and Q = (qx, qy) is to check whether the determinant of the matrix

{{qx - px, qy - py}, {rx - px, ry - py}},

namely (qx - px) * (ry - py) - (qy - py) * (rx - px) is close to 0. This solution has several related advantages over the others posted: first, it requires no special case for vertical lines, second, it doesn't divide (usually a slow operation), third, it doesn't trigger bad floating-point behavior when the line is almost, but not quite vertical.

Upvotes: 21

Sandeep Datta

Reputation: 29335

A 2D line is generally represented using an equation in two variables x and y here is a well known equation

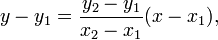
$y-y1 = (y1-y2)/(x1-x2) (x-x1)$

Now imagine your GDI+ line is drawn from (0,0) to (100, 100) then the value of m=(0-100)/(0-100) = 1 thus the equation for your line is y-0=1*(x-0) => y=x

Now that we have an equation for the line in question its easy to test if a point belongs to this line. A given point (x3, y3) belongs to this line if it satisfies the line equation when you substitute x=x3 and y=y3. For example the point (10, 10) belongs to this line since 10=10 but (10,12) does not belong to this line since 12 != 10.

NOTE: For a vertical line the value of the slope (m) is infinite but for this special case you may use the equation for a vertical line directly x=c where c = x1 = x2.

Though I have to say I am not sure if this is the most efficient way of doing this. I will try and find a more efficient way when I have some more time on hand.

Hope this helps.

Upvotes: 3