How to calculate coefficients of polynomial using Lagrange interpolation

Question

I need to calculate coefficients of polynomial using Lagrange interpolation polynomial, as my homework, I decide to do this in Javascript.

here is definition of Lagrange polynomial (L(x))

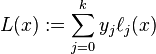
Lagrange basis polynomials are defined as follows

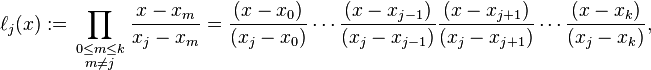
Calculate y value for specific X (W(x) function) is simple but I need to calculate coefficients of polynomial (array of [a0, a1, ..., an]) I need to do this to n<=10 but it will be nice to have arbitrary n, then I can put that function into horner function and draw that polynomial.

I have function that calculate denominator in first equation

function denominator(i, points) {
   var result = 1;
   var x_i = points[i].x;
   for (var j=points.length; j--;) {
      if (i != j) {
        result *= x_i - points[j].x;
      }
   }
   return result;
}

and function that return y using horner method (I also have drawing function using canvas)

function horner(array, x_scale, y_scale) {
   function recur(x, i, array) {
      if (i == 0) {
         return x*array[0];
      } else {
         return array[i] + x*recur(x, --i, array);
      }
   }
   return function(x) {
      return recur(x*x_scale, array.length-1, array)*y_scale;
   };
}

anybody know algorithm to do this, or idea how to calculate those coefficients

Answer 1

This code will determine the coefficients starting with the constant term.

const xPoints = [2, 4, 3, 6, 7, 10]; //example coordinates
const yPoints = [2, 5, -2, 0, 2, 8];
const coefficients = xPoints.map((_) => 0);

for (let m = 0; m < xPoints.length; m++) {
  const newCoefficients = xPoints.map((_) => 0);

  if (m > 0) {
    newCoefficients[0] = -xPoints[0] / (xPoints[m] - xPoints[0]);
    newCoefficients[1] = 1 / (xPoints[m] - xPoints[0]);
  } else {
    newCoefficients[0] = -xPoints[1] / (xPoints[m] - xPoints[1]);
    newCoefficients[1] = 1 / (xPoints[m] - xPoints[1]);
  }

  let startIndex = m === 0 ? 2 : 1;

  for (let n = startIndex; n < xPoints.length; n++) {
    if (m === n) continue;

    for (let nc = xPoints.length - 1; nc >= 1; nc--) {
      newCoefficients[nc] =
        newCoefficients[nc] * (-xPoints[n] / (xPoints[m] - xPoints[n])) +
        newCoefficients[nc - 1] / (xPoints[m] - xPoints[n]);
    }

    newCoefficients[0] =
      newCoefficients[0] * (-xPoints[n] / (xPoints[m] - xPoints[n]));
  }

  for (let nc = 0; nc < xPoints.length; nc++)
    coefficients[nc] += yPoints[m] * newCoefficients[nc];
}

Answer 2

I want to share my way of solving this problem. Perhaps it has already been demonstrated in one of the above answers, but I have not looked at them. Wrote in c++

My idea is to represent a polynomial as an array of coefficients at unknown .i-th degrees. Maybe I spoke badly, but I'll give you an example. imagine 4x^2 + 3x^1 + 5x^0 as an array [53 4]. Then if we take another array and [ 1 2 4] and multiply them by the rule X[i+j] = A[i]*B[j]. then we can get the coefficients of the new polynomial, which was obtained as a result of multiplying the past ones. I want to explain why X[ i + j]. This comes out because we multiply numbers with the same base(x) and different degrees, in which case the degrees add up. However, it's worth noting that this only works with natural numbers.

In My program, the Polinom function is responsible for multiplying polynomials.

VectorSum is responsible for adding the coefficients of two polynomials.

VectorMult is responsible for multiplying all the coefficients of a polynomial by a certain number.

Let's now consider the lagranz function.We create an empty array filled with zeros, which in the outer loop will be filled with a part of the polynomial. In the inner loop, we find the value of the SubResult polynomial by multiplying it by the SubPolinom polynomial. SubPolinom represents a value at point X that is not equal to the current iteration of the loop,((X - Xj) | i != j).

SubResult represents the coefficients of the polynomial (X-X1)(X-X2)...(X-Xn), which will appear after opening the brackets.

Then we multiply the SubResult by a certain number, which will appear as a result Yi / ( (Xi - X0)...(Xi-X(j-1))(Xi -Xj) ), where i is not equal to j. At the very end, we add up the SubResult with the previous iteration of the loop.

Thus we obtain the coefficients of the Langrange interpolation polynomial

    #include <iostream>;
#include <vector>
#include <string>
using namespace std;
vector<double> vectorSum(vector<double> A, vector<double> B) { // функция, складывающая элементы матриц при соответствующий коэф
    vector<double>result(A.size(), 0);
    if (A.size() > B.size() ){ //проверяем на одинаковость размерности матриц, если не сходятся, то увеличиваем меньшую, добавляя нули в конец
        B.resize(A.size(), 0);
    }
    else {
        A.resize(B.size(), 0);
    }
    for (int i = 0; i < A.size(); i++)
    {
        result[i] = A[i] + B[i];
    }
    return result;
}
vector<double> vectorMult( vector<double> A, double C) { // Функци, которая умножает все элементы матрицы на определенный коэф
    vector<double>result(A.size(), 0);
    for (int i = 0; i < A.size(); i++)
    {
        result[i] = A[i] * C;
    }
    return result;
}
void showPolynom(vector<double> &F) { //функция, которая выводит многочлен в привычном виде
    string res;
    for (int i = 0; i < F.size(); i++)
    {
        if (i == 0) {
            res += to_string(F[0]);
        }else if (i == 1) {
            if (F[i] == 1) {
                res+=  " + X";
            }
            else {
                res += " + " +to_string(F[i]) + "X";

            }
        }
        else {
            if (F[i] == 1) {
                res += " + X^" + to_string(i);
            }
            else {
                res += " + " + to_string(F[i]) + "X^" + to_string(i);
            }
        }
    }
    res += "\n";
    cout << res;
}
vector<double> Polinom(vector<double> &A, vector<double> &B) { // функция, которая умножает многочлен на многочлен( например (x-2)(x+2) = x^2 - 4)
    vector<double> result(A.size() + B.size() - 1, 0.0); // создаем массив, который будет размером, как максимальная степень одного плюс макс второго - 1
    for (int i = 0; i < A.size(); i++)
    {
        for (int j = 0; j < B.size(); j++)
        {   // так как позиция элемента представляет собой степеь x, а значение элемента коэф при соответсвующем x, то при умножении одного на другого степени складываются, а значения перемножаются
        }   // Приведу пример: (x + 5) = (5x^0 + 1x^1) будет представлять массив [5, 1]. Возьмем другой массив [5, 1]. на выхлде функции у нас получится массив [25, 5 + 5, 1] = [25, 10, 1]
            // Если мы проведем умножение двух многочленов вручную, то получим (x+5)(x+5) = (x^2 + 5x +5x + 25) = (x^2+10x+25), что соответветсвует массиву [25,10,1]
            result[i + j] += A[i] * B[j]; 
    }
    return result;
}
vector<double>  lagranz(vector<double> X, vector<double> Y) { //сама функция, которая считает  многочлен лангранжа 
    int size = X.size();
    vector<double> result(size, 0); // вспомогательые переменные
    vector<double> subResult;
    vector<double> subPolinom(2, 1);
    double C;
    for (int i = 0; i < size; i++)
    {
        C = Y[i]; // коэф при Yi
        subResult = { 1 }; //единичные многочлен, представляющий собой 1 
        for (int j = 0; j < size; j++)
        {
            if (i != j) {
                C /= (X[i] - X[j]); // тут мы вычисляем знаменатель П(Xi - Xj) i!=j
                subPolinom[0] = -X[j];  // создаем ногочлен (X - Xj)
                subResult = Polinom(subResult, subPolinom); //перемножаем многочлены, чтобы получить коэф. П(X - Xj) i!=j
            }
        }
        subResult = vectorMult(subResult, C); // умножаем наш многочлен на константу
        result = vectorSum(result, subResult); // складываем полученные многочлены
    }
    return result; // возвращаем коэф многочлена лангранжа
}
int main() {
    vector<double> X = { -3, -1, 3, 5 };
    vector<double> Y = { 7, -1, 4, -6};
    vector<double> result = lagranz(X, Y); // передаем значения
    showPolynom(result); // выводим результат
    return 0;
}

Answer 3

You can find coefficients of Lagrange interpolation polynomial relatively easy if you use a matrix form of Lagrange interpolation presented in "Beginner's guide to mapping simplexes affinely ", section "Lagrange interpolation". I'm afraid, I don't know JavaScript to provide you with appropriate code, but I worked with Python a little bit, maybe the following can help (sorry for bad codestyle -- I'm mathematician, not programmer)

import numpy as np
# input
x = [0, 2, 4, 5]  # <- x's
y = [2, 5, 7, 7]  # <- y's
# calculating coefficients
M = [[_x**i*(-1)**(i*len(x)) for _x in x] for i in range(len(x))]
C = [np.linalg.det((M+[y]+M)[d:d+len(x)]) for d in range(len(x)+1)]
C = (C / C[0] * (-1)**(len(x)+1) )[1:]
# polynomial lambda-function
poly = lambda _x: sum([C[i] * _x**i for i in range(len(x))])
# output and tests
print("Coefficients:\n", C)
print("TESTING:")
for _x, _y in zip(x, y):
    result = "[OK]" if np.allclose(_y, poly(_x)) else "[ERROR]"
    print(_x, " mapped to: ", poly(_x), " ; expected: ", _y, result)

This code calculates coefficients of the Lagrange interpolation polynomial, prints them, and tests that given x's are mapped into expected y's. You can test this code with Google colab, so you don't have to install anything. Probably, you can translate it to JS.

Answer 4

Well, you can do it the naive way. Represent a polynomial by the array of its coefficients, the array

[a_0,a_1,...,a_n]

corresponding to a_0 + a_1*X + ... + a_n*X^n. I'm no good with JavaScript, so pseudocode will have to do:

interpolation_polynomial(i,points)
    coefficients = [1/denominator(i,points)]
    for k = 0 to points.length-1
        if k == i
            next k
        new_coefficients = [0,0,...,0] // length k+2 if k < i, k+1 if k > i
        if k < i
            m = k
        else
            m = k-1
        for j = m downto 0
            new_coefficients[j+1] += coefficients[j]
            new_coefficients[j] -= points[k]*coefficients[j]
        coefficients = new_coefficients
    return coefficients

Start with the constant polynomial 1/((x_1-x_0)* ... *(x_i-x_{i-1})*(x_i-x_{i+1})*...*(x_i-x_n)) and multiply with X - x_k for all k != i. So that gives the coefficients for L_i, then you just multiply them with y_i (you could do that by initialising coefficients to y_i/denominator(i,points) if you pass the y-values as parameters) and add all the coefficients together finally.

polynomial = [0,0,...,0] // points.length entries
for i = 0 to points.length-1
    coefficients = interpolation_polynomial(i,points)
    for k = 0 to points.length-1
        polynomial[k] += y[i]*coefficients[k]

Calculating each L_i is O(n²), so the total calculation is O(n³).

Update: In your jsFiddle, you had an error in the polynomial multiplication loop in addition to (the now corrected) mistake with the start index I made, it should be

for (var j= (k < i) ? (k+1) : k; j--;) {
     new_coefficients[j+1] += coefficients[j];
     new_coefficients[j] -= points[k].x*coefficients[j];
}

Since you decrement j when testing, it needs to start one higher.

That doesn't produce a correct interpolation yet, but it's at least more sensible than before.

Also, in your horner function,

function horner(array, x_scale, y_scale) {
   function recur(x, i, array) {
      if (i == 0) {
         return x*array[0];
      } else {
         return array[i] + x*recur(x, --i, array);
      }
   }
   return function(x) {
      return recur(x*x_scale, array.length-1, array)*y_scale;
   };
}

you multiply the highest coefficient twice with x, it should be

if (i == 0) {
    return array[0];
}

instead. Still no good result, though.

Update2: Final typo fixes, the following works:

function horner(array, x_scale, y_scale) {
   function recur(x, i, array) {
      if (i == 0) {
         return array[0];
      } else {
         return array[i] + x*recur(x, --i, array);
      }
   }
   return function(x) {
      return recur(x*x_scale, array.length-1, array)*y_scale;
   };
}

// initialize array
function zeros(n) {
   var array = new Array(n);
   for (var i=n; i--;) {
     array[i] = 0;
   }
   return array;
}

function denominator(i, points) {
   var result = 1;
   var x_i = points[i].x;
   for (var j=points.length; j--;) {
      if (i != j) {
        result *= x_i - points[j].x;
      }
   }
    console.log(result);
   return result;
}

// calculate coefficients for Li polynomial
function interpolation_polynomial(i, points) {
   var coefficients = zeros(points.length);
    // alert("Denominator " + i + ": " + denominator(i,points));
   coefficients[0] = 1/denominator(i,points);
    console.log(coefficients[0]);
    //new Array(points.length);
   /*for (var s=points.length; s--;) {
      coefficients[s] = 1/denominator(i,points);
   }*/
   var new_coefficients;

   for (var k = 0; k<points.length; k++) {
      if (k == i) {
        continue;
      }
      new_coefficients = zeros(points.length);
       for (var j= (k < i) ? k+1 : k; j--;) {
         new_coefficients[j+1] += coefficients[j];
         new_coefficients[j] -= points[k].x*coefficients[j];
      }   
      coefficients = new_coefficients;
   }
   console.log(coefficients);
   return coefficients;
}

// calculate coefficients of polynomial
function Lagrange(points) {
   var polynomial = zeros(points.length);
   var coefficients;
   for (var i=0; i<points.length; ++i) {
     coefficients = interpolation_polynomial(i, points);
     //console.log(coefficients);
     for (var k=0; k<points.length; ++k) {
       // console.log(points[k].y*coefficients[k]);
        polynomial[k] += points[i].y*coefficients[k];
     }
   }
   return polynomial;
}