CODEWITHSUNDEEP
loggingplotwolfram-mathematica
Tyson Williams
Tyson Williams

Reputation: 1725

Exponential form of tick marks for log plot in Mathematica

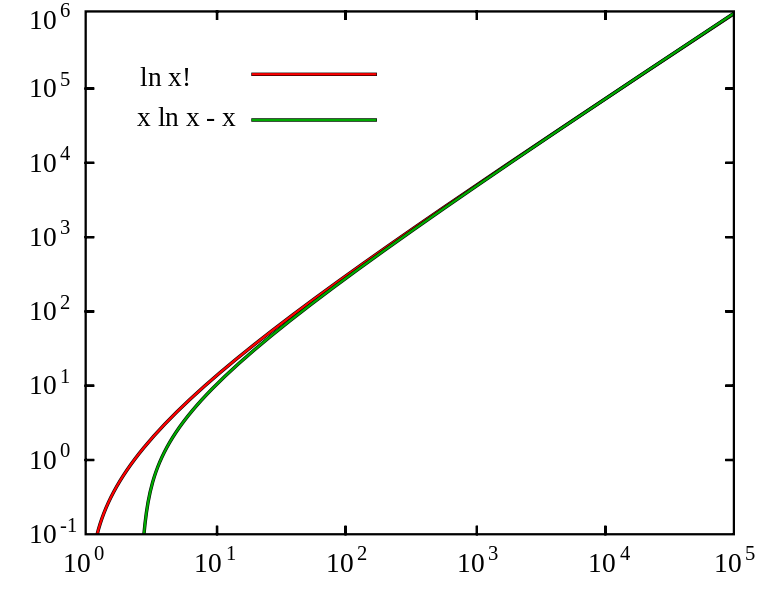
In an attempt to learn more Mathematica, I am trying to reproduce the tick marks on this log (log) plot: enter image description here

This is as close as I can get:

LogLogPlot[Log[x!], {x, 1, 10^5}, PlotRange -> {{0, 10^5}, {10^-1, 10^6}}, Ticks -> {Table[10^i, {i, 0, 5}], Table[10^i, {i, -1, 6}]}]

enter image description here

Question

How can I make tick marks that are always of the form 10^n for appropriate values of n?

Upvotes: 14

Views: 9142

Answers (4)

abcd
abcd

Reputation: 42225

LevelScheme is a package for Mathematica that makes making such plots very easy, fully customizable and professional looking. I'm very certain that if your plot was made in mathematica, it was using LevelScheme. Here's my reproduction of your plot in Mathematica using LevelScheme

<<LevelScheme`;
Figure[{
    FigurePanel[{{0,1},{0,1}},
            PlotRange->{{0,5},{-1,6}},
            FrameTicks->{
                        LogTicks[0,5,ShowMinorTicks->False],
                        LogTicks[-1,6,ShowMinorTicks->False]
                    }
    ],
    RawGraphics[
        LogLogPlot[{Log[x!],x Log[x]-x},{x,1,10^5},
                PlotRange->{{0,10^5},{10^-1,10^6}},
                PlotStyle->Darker/@{Red,Green}
            ]
    ]
}, PlotRange->{{-0.1,1.04},{-0.05,1.025}},ImageSize->300{1,1}]

enter image description here

Upvotes: 3

Heike
Heike

Reputation: 24420

To expand on the previous answers, you can calculate the right range for the Tables in the Ticks option automatically by doing something like

ticksfun[xmin_, xmax_] := 
 Table[{10^i, Superscript[10, i]}, {i, Floor[Log10[xmin]], 
   Ceiling[Log10[xmax]]}]

LogLogPlot[Log[x!], {x, 1, 10^5}, 
 PlotRange -> {{0, 10^5}, {10^-1, 10^6}}, 
 Ticks -> {ticksfun, ticksfun}]

Upvotes: 4

Brett Champion
Brett Champion

Reputation: 8567

Superscript, the generic typesetting form without any built-in meaning, is your friend for this.

LogLogPlot[Log[x!], {x, 1, 10^5}, 
   PlotRange -> {{0, 10^5}, {10^-1, 10^6}}, 
   Ticks -> {
       Table[{10^i, Superscript[10, i]}, {i, 0, 5}], 
       Table[{10^i, Superscript[10, i]}, {i, -1, 6}]
       }
   ]

Upvotes: 14

Sebastian Paaske T&#248;rholm
Sebastian Paaske T&#248;rholm

Reputation: 50858

You can specify the label for a given tick, by giving a 2-tuple of {value, label} instead of giving just giving a value.

This still leaves us with the conundrum of how to maintain the 10^n-form. To do this, we observe, that using Defer makes the 10^i retain its form. However, we still need to Evaluate the i inside of it, as otherwise we just get a bunch of 10^i-labels.

Example:

In[19]:= Table[10^i, {i, 0, 6}]

Out[19]= {1, 10, 100, 1000, 10000, 100000, 1000000}

In[18]:= Table[10^Defer[i], {i, 0, 6}]

Out[18]= {10^i, 10^i, 10^i, 10^i, 10^i, 10^i, 10^i}

In[17]:= Table[10^Defer[Evaluate[i]], {i, 0, 6}]

Out[17]= {10^0, 10^1, 10^2, 10^3, 10^4, 10^5, 10^6}

Using this, we can now do the following to get a solution:

LogLogPlot[Log[x!], {x, 1, 10^5}, 
 PlotRange -> {{0, 10^5}, {10^-1, 10^6}}, 
 Ticks -> {Table[{10^i, 10^Defer[Evaluate [i]]}, {i, 0, 5}], 
   Table[{10^i, 10^Defer[Evaluate [i]]}, {i, -1, 6}]}, 
 TicksStyle -> StandardForm]

Upvotes: 2

Related Questions